Fractals in nature

Fractal(lat. fractus- crushed) is a term meaning a geometric figure that has the property of self-similarity, that is, composed of several parts, each of which is similar to the entire figure.

Nature often creates amazing and beautiful fractals, with ideal geometry and such harmony that you simply freeze with admiration.
From giant mountains to what we eat for lunch, perfect harmony can be seen everywhere.
Sea shells
Nautilus is one of the most famous examples of a fractal in nature.

Snowflakes

Lightning
Lightning terrifies and frightens and at the same time delights with its beauty. Fractals created by lightning are not arbitrary or regular.

Romanessa
This special type of broccoli, a cruciferous and tasty cousin of cabbage, is a particularly symmetrical fractal. You can prepare it for your favorite math teacher.

Fern
Fern is a good example of a fractal among flora

Queen Anne's Lace
Queen Anne's Lace wild carrot is a perfect example of a floral fractal. Each constellation is copied exactly the same, only smaller. The photo was taken from below to see it in all its glory.

Broccoli
Although broccoli is not as famously geometric as romanessa, it is also fractal.

Peacock
Peacocks are known to everyone for their colorful plumage, in which solid fractals are hidden. Have you ever seen an albino peacock? Look

A pineapple
Pineapple is an unusual fruit; it is, in fact, a fractal. Although it is often associated with Hawaii, the fruit is native to southern Brazil.

Clouds
Look out the window now. Almost at any moment you can see fractals in the sky.

Crystals
Ice, frosty patterns on windows are also fractals

Mountains
Mountain crevices and coastlines, although arbitrary in their lines, are also fractal

Trees and leaves
From an enlarged image of a leaf to the branches of a tree - fractals can be found in everything

Coastline

Individual fragments of the coast create fractality. And this is Florida

Rivers and fjords
From the western United States of America to the icy fjords of Norway, airline passengers can see it all. And we thank some for having the courage to photograph such beauty.

Sea urchins and starfish

Sea urchins are so small and compact, as if they came from the hand of a skilled jeweler. But who will surpass nature? And starfish are like a reflection of the heavenly ones

Stalagmites and stalactites

While stalagmites rise from the ground, stalactites reach towards it

Often, brilliant discoveries made in science can radically change our lives. For example, the invention of a vaccine can save many people, but the creation of new weapons leads to murder. Literally yesterday (on the scale of history) man “tamed” electricity, and today he can no longer imagine his life without it. However, there are also discoveries that, as they say, remain in the shadows, despite the fact that they also have one or another impact on our lives. One of these discoveries was the fractal. Most people have never even heard of this concept and will not be able to explain its meaning. In this article we will try to understand the question of what a fractal is and consider the meaning of this term from the perspective of science and nature.

Order in chaos

In order to understand what a fractal is, we should begin the debriefing from the position of mathematics, but before delving into it, we will philosophize a little. Every person has a natural curiosity, thanks to which he learns about the world around him. Often, in his quest for knowledge, he tries to use logic in his judgments. Thus, by analyzing the processes that occur around him, he tries to calculate relationships and derive certain patterns. The greatest minds on the planet are busy solving these problems. Roughly speaking, our scientists are looking for patterns where there are none, and there should not be any. And yet, even in chaos there is a connection between certain events. This connection is what the fractal is. As an example, consider a broken branch lying on the road. If we look closely at it, we will see that with all its branches and twigs it itself looks like a tree. This similarity of a separate part with a single whole indicates the so-called principle of recursive self-similarity. Fractals can be found all over the place in nature, because many inorganic and organic forms are formed in a similar way. These are clouds, sea shells, snail shells, tree crowns, and even the circulatory system. This list can be continued indefinitely. All these random shapes are easily described by a fractal algorithm. Now we have come to consider what a fractal is from the perspective of exact sciences.

Some dry facts

The word “fractal” itself is translated from Latin as “partial”, “divided”, “fragmented”, and as for the content of this term, there is no formulation as such. It is usually interpreted as a self-similar set, a part of the whole, which repeats its structure at the micro level. This term was coined in the seventies of the twentieth century by Benoit Mandelbrot, who is recognized as the father. Today, the concept of fractal means a graphic image of a certain structure, which, when enlarged, will be similar to itself. However, the mathematical basis for the creation of this theory was laid even before the birth of Mandelbrot himself, but it could not develop until electronic computers appeared.

Historical background, or How it all began

At the turn of the 19th and 20th centuries, the study of the nature of fractals was sporadic. This is explained by the fact that mathematicians preferred to study objects that could be researched on the basis of general theories and methods. In 1872, the German mathematician K. Weierstrass constructed an example of a continuous function that is not differentiable anywhere. However, this construction turned out to be entirely abstract and difficult to perceive. Next came the Swede Helge von Koch, who in 1904 constructed a continuous curve that had no tangent anywhere. It's fairly easy to draw and turns out to have fractal properties. One of the variants of this curve was named after its author - “Koch snowflake”. Further, the idea of ​​self-similarity of figures was developed by the future mentor of B. Mandelbrot, the Frenchman Paul Levy. In 1938, he published the article "Plane and spatial curves and surfaces consisting of parts similar to the whole." In it, he described a new type - the Lewy C-curve. All of the above figures are conventionally classified as geometric fractals.

Dynamic or algebraic fractals

The Mandelbrot set belongs to this class. The first researchers in this direction were the French mathematicians Pierre Fatou and Gaston Julia. In 1918, Julia published a paper based on the study of iterations of rational complex functions. Here he described a family of fractals that are closely related to the Mandelbrot set. Despite the fact that this work glorified the author among mathematicians, it was quickly forgotten. And only half a century later, thanks to computers, Julia’s work received a second life. Computers made it possible to make visible to every person the beauty and richness of the world of fractals that mathematicians could “see” by displaying them through functions. Mandelbrot was the first to use a computer to carry out calculations (such a volume cannot be done manually) that made it possible to construct an image of these figures.

A person with spatial imagination

Mandelbrot began his scientific career at IBM Research Center. While studying the possibilities of transmitting data over long distances, scientists were faced with the fact of large losses that arose due to noise interference. Benoit was looking for ways to solve this problem. Looking through the measurement results, he noticed a strange pattern, namely: the noise graphs looked the same on different time scales.

A similar picture was observed both for a period of one day and for seven days or for an hour. Benoit Mandelbrot himself often repeated that he does not work with formulas, but plays with pictures. This scientist was distinguished by imaginative thinking; he translated any algebraic problem into the geometric area, where the correct answer is obvious. So it is not surprising that he is distinguished by his wealth and became the father of fractal geometry. After all, awareness of this figure can only come when you study the drawings and think about the meaning of these strange swirls that form the pattern. Fractal patterns do not have identical elements, but they are similar at any scale.

Julia - Mandelbrot

One of the first drawings of this figure was a graphic interpretation of the set, which was born out of the work of Gaston Julia and was further developed by Mandelbrot. Gaston tried to imagine what a set would look like based on a simple formula that was iterated through a feedback loop. Let's try to explain what has been said in human language, so to speak, on the fingers. For a specific numerical value, we find a new value using a formula. We substitute it into the formula and find the following. The result is large. To represent such a set it is necessary to perform this operation a huge number of times: hundreds, thousands, millions. This is what Benoit did. He processed the sequence and transferred the results to graphical form. Subsequently, he colored the resulting figure (each color corresponds to a certain number of iterations). This graphic image was named “Mandelbrot fractal”.

L. Carpenter: art created by nature

The theory of fractals quickly found practical application. Since it is very closely related to the visualization of self-similar images, artists were the first to adopt the principles and algorithms for constructing these unusual forms. The first of them was the future founder of Pixar, Lauren Carpenter. While working on a presentation of aircraft prototypes, he came up with the idea of ​​using an image of mountains as a background. Today, almost every computer user can cope with such a task, but in the seventies of the last century, computers were not able to perform such processes, because there were no graphic editors or applications for three-dimensional graphics at that time. And then Loren came across Mandelbrot’s book “Fractals: Form, Randomness and Dimension.” In it, Benoit gave many examples, showing that fractals exist in nature (fyva), he described their varied shapes and proved that they are easily described by mathematical expressions. The mathematician cited this analogy as an argument for the usefulness of the theory he was developing in response to a barrage of criticism from his colleagues. They argued that a fractal is just a pretty picture, has no value, and is a by-product of the work of electronic machines. Carpenter decided to try this method in practice. After carefully studying the book, the future animator began to look for a way to implement fractal geometry in computer graphics. It took him only three days to render a completely realistic image of the mountain landscape on his computer. And today this principle is widely used. As it turns out, creating fractals does not take much time and effort.

Carpenter's solution

The principle Lauren used was simple. It consists of dividing larger ones into small elements, and those into similar smaller ones, and so on. Carpenter, using large triangles, split them into 4 small ones, and so on, until he had a realistic mountain landscape. Thus, he became the first artist to use a fractal algorithm in computer graphics to construct the required image. Today this principle is used to imitate various realistic natural forms.

The first 3D visualization using a fractal algorithm

A few years later, Lauren applied his developments in a large-scale project - the animated video Vol Libre, shown on Siggraph in 1980. This video shocked many, and its creator was invited to work at Lucasfilm. Here the animator was able to realize his full potential; he created three-dimensional landscapes (an entire planet) for the feature film "Star Trek". Any modern program (“Fractals”) or application for creating 3D graphics (Terragen, Vue, Bryce) uses the same algorithm for modeling textures and surfaces.

Tom Beddard

Formerly a laser physicist and now a digital artist and artist, Beddard created a number of very intriguing geometric shapes, which he called Fabergé fractals. Outwardly, they resemble decorative eggs from a Russian jeweler; they have the same brilliant, intricate pattern. Beddard used a template method to create his digital renderings of the models. The resulting products amaze with their beauty. Although many refuse to compare a handmade product with a computer program, it must be admitted that the resulting forms are extremely beautiful. The highlight is that anyone can build such a fractal using the WebGL software library. It allows you to explore various fractal structures in real time.

Fractals in nature

Few people pay attention, but these amazing figures are present everywhere. Nature is created from self-similar figures, we just don’t notice it. It is enough to look through a magnifying glass at our skin or a leaf of a tree, and we will see fractals. Or take, for example, a pineapple or even a peacock's tail - they consist of similar figures. And the Romanescu broccoli variety is generally striking in its appearance, because it can truly be called a miracle of nature.

Musical pause

It turns out that fractals are not only geometric shapes, they can also be sounds. Thus, musician Jonathan Colton writes music using fractal algorithms. It claims to correspond to natural harmony. The composer publishes all of his works under a CreativeCommons Attribution-Noncommercial license, which provides for free distribution, copying, and transfer of works to others.

Fractal indicator

This technique has found a very unexpected application. On its basis, a tool for analyzing the stock exchange market was created, and, as a result, it began to be used in the Forex market. Nowadays, the fractal indicator is found on all trading platforms and is used in a trading technique called price breakout. This technique was developed by Bill Williams. As the author comments on his invention, this algorithm is a combination of several “candles”, in which the central one reflects the maximum or, conversely, the minimum extreme point.

Finally

So we looked at what a fractal is. It turns out that in the chaos that surrounds us, there actually exist ideal forms. Nature is the best architect, ideal builder and engineer. It is arranged very logically, and if we cannot find a pattern, this does not mean that it does not exist. Maybe we need to look on a different scale. We can say with confidence that fractals still hold many secrets that we have yet to discover.

Nature is a perfect creation, scientists are convinced, who discover the proportions of the golden section in the structure of the human body, and fractal figures in the head of a cauliflower.

“The study and observation of nature gave birth to science,” wrote Cicero in the first century BC. In later times, with the development of science and its distance from the study of nature, scientists are surprised to discover what was known to our ancestors, but was not confirmed by scientific methods.

It is interesting to find similar formations in the micro- and macrocosm; it can also be inspiring that science can describe the geometry of these formations. The circulatory system, a river, lightning, tree branches... all of these are similar systems, consisting of different particles and different in scale.

Proportions of the “golden ratio”

Even the ancient Greeks, and possibly the Egyptians, knew the proportion of the “golden section”. Luca Pacioli, a Renaissance mathematician, called this ratio the “divine proportion.” Later, scientists discovered that the golden ratio, which is so pleasing to the human eye and which is often found in classical architecture, art and even poetry, can be found everywhere in nature.

The golden ratio is a division of a segment into two unequal parts, in which the short part is related to the long one as the long part is to the entire segment. The ratio of the long part to the entire segment is an infinite number, an irrational fraction 0.618..., the ratio of the short part is 0.382...

If you build a rectangle with sides whose ratio is equal to the proportion of the “golden ratio”, and inscribe another “golden rectangle” into it, another one into that one, and so on ad infinitum inwards and outwards, then a spiral can be drawn along the corner points of the rectangles. It is interesting that such a spiral will coincide with a cut of a nautilus shell, as well as other spirals found in nature.

Illustration: Homk/wikipedia.org

Nautilus fossil.
Photo: Studio-Annika/Photos.com

Nautilus shell.
Photo: Chris 73/en.wikipedia.org

The proportion of the golden ratio is perceived by the human eye as beautiful and harmonious. And the proportion 0.618... is equal to the ratio of the previous to the next number in the Fibonacci series. Fibonacci numbers appear everywhere in nature: this is the spiral along which the branches of a plant adjoin the stem, the spiral along which the scales on a pine cone grow or the grains on a sunflower. Interestingly, the number of rows spinning counterclockwise and clockwise are adjacent numbers in the Fibonacci series.

The head of a broccoli cabbage and a ram's horn twists in a spiral... And in the human body itself, of course, healthy and of normal proportions, the golden ratio ratios are found.

Vitruvian Man. Drawing by Leonardo da Vinci.

1, 1, 2, 3, 5, 8, 13, 21, ... are numbers in the Fibonacci series, in which each subsequent term is obtained from the sum of the previous two. Distant spiral galaxies photographed by satellites also spin in Fibonacci spirals.

Spiral galaxy.
Photo: NASA

Three tropical cyclones.
Photo: NASA

The DNA molecule is twisted in a double helix.

Twisted human DNA.
Illustration: Zephyris/en.wikipedia.org

The hurricane twists in a spiral, the spider weaves its web in a spiral.

Web of a cross spider.
Photo: Vincent de Groot/videgro.net

The “golden proportion” can also be seen in the body structure of the butterfly, in relation to the thoracic and abdominal parts of its body, as well as in the dragonfly. And most eggs fit, if not into the rectangle of the golden ratio, then into a derivative of it.

Illustration: Adolphe Millot

Fractals

Other interesting shapes that we can see everywhere in nature are fractals. Fractals are shapes made up of parts, each of which is similar to the whole shape - isn't this reminiscent of the principle of the golden ratio?

Trees, lightning, bronchi and the human circulatory system have a fractal shape; ferns and broccoli are also called ideal natural illustrations of fractals. “Everything is so complicated, everything is so simple” is how nature works, people notice, listening to it with respect.

“Nature has endowed man with the desire to discover the truth,” wrote Cicero, with whose words I would like to end the first part of the article on geometry in nature.

Broccoli is a perfect natural illustration of a fractal.
Photo: pdphoto.org

Fern leaves have the shape of a fractal figure - they are self-similar.
Photo: Stockbyte/Photos.com

Green fractals: fern leaves.
Photo: John Foxx/Photos.com

Veins on a yellowed leaf, shaped like a fractal.
Photo: Diego Barucco/Photos.com

Cracks on a stone: fractal in macro.
Photo: Bob Beale/Photos.com

Branches of the circulatory system on the ears of a rabbit.
Photo: Lusoimages/Photos.com

Lightning strike - fractal branch.
Photo: John R. Southern/flickr.com

Branch of arteries in the human body.

The winding river and its branches.
Photo: Jupiterimages/Photos.com

Ice frozen on glass has a self-similar pattern.
Photo: Schnobby/en.wikipedia.org

An ivy leaf with branching veins - fractal in shape.
Photo: Wojciech Plonka/Photos.com

What do a tree, a seashore, a cloud, or the blood vessels in our hand have in common? There is one property of structure that is inherent in all of the listed objects: they are self-similar. From a branch, as from a tree trunk, smaller shoots extend, from them even smaller ones, etc., that is, a branch is similar to the whole tree. The circulatory system is structured in a similar way: arterioles depart from the arteries, and from them the smallest capillaries through which oxygen enters the organs and tissues. Let's look at satellite images of the sea coast: we will see bays and peninsulas; Let's look at it, but from a bird's eye view: we will see bays and capes; Now imagine that we are standing on the beach and looking at our feet: there will always be pebbles that protrude further into the water than the rest. That is, the coastline, when zoomed in, remains similar to itself. The American (although he grew up in France) mathematician Benoit Mandelbrot called this property of objects fractality, and such objects themselves - fractals (from the Latin fractus - broken).

There is an interesting story connected with the coastline, or more precisely, with the attempt to measure its length, which formed the basis of Mandelbrot’s scientific article, and is also described in his book “The Fractal Geometry of Nature.” We are talking about an experiment carried out by Lewis Fry Richardson, a very talented and eccentric mathematician, physicist and meteorologist. One of the directions of his research was an attempt to find a mathematical description of the causes and likelihood of an armed conflict between two countries. Among the parameters that he took into account was the length of the common border of the two warring countries. When he collected data for numerical experiments, he discovered that data on the common border of Spain and Portugal differed greatly from different sources. This prompted him to the following discovery: the length of a country's borders depends on the ruler with which we measure them. The smaller the scale, the longer the border. This is due to the fact that with greater magnification it becomes possible to take into account more and more new bends of the coast, which were previously ignored due to the coarseness of the measurements. And if with each increase in scale previously unaccounted for bends of lines are revealed, then it turns out that the length of the boundaries is infinite! True, this does not actually happen - the accuracy of our measurements has a finite limit. This paradox is called the Richardson effect.

Nowadays, the theory of fractals is widely used in various areas of human activity. In addition to fractal painting, fractals are used in information theory to compress graphic data (the property of self-similarity of fractals is mainly used here - after all, to remember a small fragment of a picture and the transformations with which you can obtain the remaining parts, much less memory is required than to store the entire file). By adding random disturbances to the formulas that define a fractal, you can obtain stochastic fractals that very plausibly convey some real objects - relief elements, the surface of reservoirs, some plants, which is successfully used in physics, geography and computer graphics to achieve greater similarity of simulated objects with real. In radio electronics, in the last decade, antennas with a fractal shape began to be produced. Taking up little space, they provide high-quality signal reception. And economists use fractals to describe currency rate fluctuation curves (this property was discovered by Mandelbrot more than 30 years ago).

The most ingenious discoveries in science can radically change human life. The invented vaccine can save millions of people; the creation of weapons, on the contrary, takes away these lives. More recently (on the scale of human evolution) we have learned to “tame” electricity - and now we cannot imagine life without all these convenient devices that use electricity. But there are also discoveries that few people attach importance to, although they also greatly influence our lives.

One of these “inconspicuous” discoveries is fractals. You've probably heard this catchy word before, but do you know what it means and how much interesting information is hidden in this term?

Every person has a natural curiosity, a desire to understand the world around him. And in this endeavor, a person tries to adhere to logic in judgments. Analyzing the processes taking place around him, he tries to find the logic of what is happening and derive some pattern. The greatest minds on the planet are busy with this task. Roughly speaking, scientists are looking for a pattern where there shouldn't be one. Nevertheless, even in chaos it is possible to find connections between events. And this connection is a fractal.

Our little daughter, four and a half years old, is now at that wonderful age when the number of questions “Why?” many times exceeds the number of answers that adults manage to give. Not long ago, while examining a branch raised from the ground, my daughter suddenly noticed that this branch, with its twigs and branches, itself looked like a tree. And, of course, what followed was the usual question “Why?”, to which parents had to look for a simple explanation that the child could understand.

The similarity of a single branch with a whole tree discovered by a child is a very accurate observation, which once again testifies to the principle of recursive self-similarity in nature. Many organic and inorganic forms in nature are formed in a similar way. Clouds, sea shells, a snail’s “house,” the bark and crown of trees, the circulatory system, and so on—the random shapes of all these objects can be described by a fractal algorithm.

⇡ Benoit Mandelbrot: father of fractal geometry

The word “fractal” itself appeared thanks to the brilliant scientist Benoit B. Mandelbrot.

He himself coined the term in the 1970s, borrowing the word fractus from Latin, where it literally means “broken” or “crushed.” What is it? Today, the word “fractal” most often means a graphic representation of a structure that, on a larger scale, is similar to itself.

The mathematical basis for the emergence of the theory of fractals was laid many years before the birth of Benoit Mandelbrot, but it could only develop with the advent of computing devices. At the beginning of his scientific career, Benoit worked at the IBM research center. At that time, the center's employees were working on transmitting data over a distance. During the research, scientists were faced with the problem of large losses arising from noise interference. Benoit had a difficult and very important task - to understand how to predict the occurrence of noise interference in electronic circuits when the statistical method turns out to be ineffective.

Looking through the results of noise measurements, Mandelbrot noticed one strange pattern - the noise graphs at different scales looked the same. An identical pattern was observed regardless of whether it was a noise graph for one day, a week, or an hour. It was necessary to change the scale of the graph, and the picture was repeated every time.

During his lifetime, Benoit Mandelbrot repeatedly said that he did not study formulas, but simply played with pictures. This man thought very figuratively, and translated any algebraic problem into the field of geometry, where, according to him, the correct answer is always obvious.

It is not surprising that it was a man with such a rich spatial imagination who became the father of fractal geometry. After all, awareness of the essence of fractals comes precisely when you begin to study the drawings and think about the meaning of strange swirl patterns.

A fractal pattern does not have identical elements, but is similar on any scale. It was previously simply impossible to construct such an image with a high degree of detail manually; this required a huge amount of calculations. For example, the French mathematician Pierre Joseph Louis Fatou described this set more than seventy years before Benoit Mandelbrot's discovery. If we talk about the principles of self-similarity, they were mentioned in the works of Leibniz and Georg Cantor.

One of the first fractal drawings was a graphical interpretation of the Mandelbrot set, which was born thanks to the research of Gaston Maurice Julia.

Gaston Julia (always wearing a mask - injury from World War I)

This French mathematician wondered what a set would look like if it were constructed from a simple formula iterated through a feedback loop. If we explain it “on our fingers,” this means that for a specific number we find a new value using the formula, after which we substitute it again into the formula and get another value. The result is a large sequence of numbers.

To get a complete picture of such a set, you need to do a huge number of calculations - hundreds, thousands, millions. It was simply impossible to do this manually. But when powerful computing devices became available to mathematicians, they were able to take a fresh look at formulas and expressions that had long been of interest. Mandelbrot was the first to use a computer to calculate a classical fractal. After processing a sequence consisting of a large number of values, Benoit plotted the results on a graph. That's what he got.

Subsequently, this image was colored (for example, one of the methods of coloring is by the number of iterations) and became one of the most popular images ever created by man.

As the ancient saying attributed to Heraclitus of Ephesus says, “You cannot step into the same river twice.” It is perfectly suited for interpreting the geometry of fractals. No matter how detailed we look at a fractal image, we will always see a similar pattern.

Those wishing to see what an image of Mandelbrot space would look like when zoomed in many times over can do so by downloading the animated GIF.

⇡ Lauren Carpenter: art created by nature

The theory of fractals soon found practical application. Since it is closely related to the visualization of self-similar images, it is not surprising that the first to adopt algorithms and principles for constructing unusual forms were artists.

The future co-founder of the legendary Pixar studio, Loren C. Carpenter, began working in 1967 at Boeing Computer Services, which was one of the divisions of the famous corporation developing new aircraft.

In 1977, he created presentations with prototype flying models. Loren's responsibilities included developing images of the aircraft being designed. He had to create pictures of new models, showing future aircraft from different angles. At some point, the future founder of Pixar Animation Studios came up with the creative idea of ​​using an image of mountains as a background. Today, any schoolchild can solve such a problem, but in the late seventies of the last century, computers could not cope with such complex calculations - there were no graphic editors, not to mention applications for 3D graphics. In 1978, Lauren accidentally saw Benoit Mandelbrot's book Fractals: Form, Chance and Dimension in a store. What caught his attention in this book was that Benoit gave a lot of examples of fractal shapes in real life and argued that they can be described by a mathematical expression.

This analogy was not chosen by the mathematician by chance. The fact is that as soon as he published his research, he had to face a whole barrage of criticism. The main thing that his colleagues reproached him for was the uselessness of the theory being developed. “Yes,” they said, “these are beautiful pictures, but nothing more. The theory of fractals has no practical value.” There were also those who generally believed that fractal patterns were simply a by-product of the work of the “devilish machines”, which in the late seventies seemed to many to be something too complex and unexplored to be completely trusted. Mandelbrot tried to find obvious applications for fractal theory, but in the grand scheme of things he didn't need to. Over the next 25 years, the followers of Benoit Mandelbrot proved the enormous benefits of such a “mathematical curiosity,” and Lauren Carpenter was one of the first to try the fractal method in practice.

After studying the book, the future animator seriously studied the principles of fractal geometry and began to look for a way to implement it in computer graphics. In just three days of work, Lauren was able to render a realistic image of the mountain system on his computer. In other words, he used formulas to paint a completely recognizable mountain landscape.

The principle that Lauren used to achieve her goal was very simple. It consisted of dividing a larger geometric figure into small elements, and these, in turn, were divided into similar figures of a smaller size.

Using larger triangles, Carpenter split them into four smaller ones and then repeated this process over and over again until he had a realistic mountain landscape. Thus, he managed to become the first artist to use a fractal algorithm for constructing images in computer graphics. As soon as word of the work became known, enthusiasts around the world took up the idea and began using the fractal algorithm to imitate realistic natural shapes.

One of the first 3D visualizations using a fractal algorithm

Just a few years later, Lauren Carpenter was able to apply his developments in a much larger project. The animator created a two-minute demo of Vol Libre from them, which was shown on Siggraph in 1980. This video shocked everyone who saw it, and Lauren received an invitation from Lucasfilm.

The animation was rendered on a VAX-11/780 computer from Digital Equipment Corporation with a clock speed of five megahertz, and each frame took about half an hour to render.

Working for Lucasfilm Limited, the animator created 3D landscapes using the same scheme for the second full-length film in the Star Trek saga. In The Wrath of Khan, Carpenter was able to create an entire planet using the same principle of fractal surface modeling.

Currently, all popular applications for creating 3D landscapes use a similar principle for generating natural objects. Terragen, Bryce, Vue and other 3D editors rely on a fractal algorithm for modeling surfaces and textures.

⇡ Fractal antennas: less is more

Over the past half century, life has rapidly begun to change. Most of us take the advances of modern technology for granted. You get used to everything that makes life more comfortable very quickly. Rarely does anyone ask the questions “Where did this come from?” and “How does it work?” A microwave heats up breakfast - great, a smartphone gives you the opportunity to talk to another person - great. This seems like an obvious possibility to us.

But life could have been completely different if a person had not sought an explanation for the events taking place. Take cell phones, for example. Remember the retractable antennas on the first models? They interfered, increased the size of the device, and in the end, often broke. We believe they have sunk into oblivion forever, and part of the reason for this is... fractals.

Fractal patterns fascinate with their patterns. They definitely resemble images of cosmic objects - nebulae, galaxy clusters, and so on. It is therefore quite natural that when Mandelbrot voiced his theory of fractals, his research aroused increased interest among those who studied astronomy. One of these amateurs named Nathan Cohen, after attending a lecture by Benoit Mandelbrot in Budapest, was inspired by the idea of ​​​​practical application of the acquired knowledge. True, he did this intuitively, and chance played an important role in his discovery. As a radio amateur, Nathan sought to create an antenna with the highest possible sensitivity.

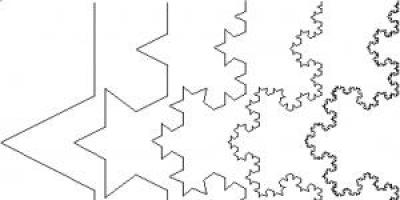
The only way to improve the parameters of the antenna, which was known at that time, was to increase its geometric dimensions. However, the owner of the property in downtown Boston that Nathan rented was categorically against installing large devices on the roof. Then Nathan began experimenting with different antenna shapes, trying to get the maximum result with the minimum size. Inspired by the idea of ​​fractal forms, Cohen, as they say, randomly made one of the most famous fractals from wire - the “Koch snowflake”. Swedish mathematician Helge von Koch came up with this curve back in 1904. It is obtained by dividing a segment into three parts and replacing the middle segment with an equilateral triangle without a side coinciding with this segment. The definition is a little difficult to understand, but in the figure everything is clear and simple.

There are also other variations of the Koch curve, but the approximate shape of the curve remains similar

When Nathan connected the antenna to the radio receiver, he was very surprised - the sensitivity increased dramatically. After a series of experiments, the future professor at Boston University realized that an antenna made according to a fractal pattern has high efficiency and covers a much wider frequency range compared to classical solutions. In addition, the shape of the antenna in the form of a fractal curve makes it possible to significantly reduce the geometric dimensions. Nathan Cohen even came up with a theorem proving that to create a broadband antenna, it is enough to give it the shape of a self-similar fractal curve.

The author patented his discovery and founded a company for the development and design of fractal antennas Fractal Antenna Systems, rightly believing that in the future, thanks to his discovery, cell phones will be able to get rid of bulky antennas and become more compact.

In principle, this is what happened. True, to this day Nathan is engaged in a legal battle with large corporations that are illegally using his discovery to produce compact communication devices. Some well-known mobile device manufacturers, such as Motorola, have already reached an amicable agreement with the inventor of the fractal antenna.

⇡ Fractal dimensions: you can’t understand it with your mind

Benoit borrowed this question from the famous American scientist Edward Kasner.

The latter, like many other famous mathematicians, loved to communicate with children, asking them questions and receiving unexpected answers. Sometimes this led to surprising consequences. For example, the nine-year-old nephew of Edward Kasner came up with the now well-known word “googol,” meaning one followed by one hundred zeros. But let's return to fractals. The American mathematician liked to ask the question how long is the US coastline. After listening to the opinion of his interlocutor, Edward himself spoke the correct answer. If you measure the length on a map using broken segments, the result will be inaccurate, because the coastline has a large number of irregularities. What happens if we measure as accurately as possible? You will have to take into account the length of each unevenness - you will need to measure every cape, every bay, rock, the length of a rocky ledge, a stone on it, a grain of sand, an atom, and so on. Since the number of irregularities tends to infinity, the measured length of the coastline will increase to infinity when measuring each new irregularity.

The smaller the measure when measuring, the longer the measured length

Interestingly, following Edward's prompts, the children were much faster than the adults in saying the correct solution, while the latter had trouble accepting such an incredible answer.

Using this problem as an example, Mandelbrot proposed using a new approach to measurements. Since the coastline is close to a fractal curve, it means that a characterizing parameter can be applied to it - the so-called fractal dimension.

What a regular dimension is is clear to anyone. If the dimension is equal to one, we get a straight line, if two - a flat figure, three - a volume. However, this understanding of dimension in mathematics does not work with fractal curves, where this parameter has a fractional value. Fractal dimension in mathematics can be conventionally considered as a “roughness”. The higher the roughness of the curve, the greater its fractal dimension. A curve that, according to Mandelbrot, has a fractal dimension higher than its topological dimension has an approximated extent that does not depend on the number of dimensions.

Currently, scientists are finding more and more areas to apply the theory of fractals. Using fractals, you can analyze fluctuations in stock exchange prices, study all sorts of natural processes, such as fluctuations in the number of species, or simulate the dynamics of flows. Fractal algorithms can be used for data compression, such as image compression. And by the way, to get a beautiful fractal on your computer screen, you don’t have to have a doctorate.

⇡ Fractal in the browser

Perhaps one of the easiest ways to get a fractal pattern is to use an online vector editor from the young talented programmer Toby Schachman. The tools of this simple graphic editor are based on the same principle of self-similarity.

At your disposal there are only two simplest shapes - a quadrangle and a circle. You can add them to the canvas, scale them (to scale along one of the axes, hold down the Shift key) and rotate them. Overlapping according to the principle of Boolean addition operations, these simplest elements form new, less trivial forms. These new shapes can then be added to the project, and the program will repeat generating these images ad infinitum. At any stage of working on a fractal, you can return to any component of a complex shape and edit its position and geometry. A fun activity, especially when you consider that the only tool you need to create is a browser. If you do not understand the principle of working with this recursive vector editor, we advise you to watch the video on the official website of the project, which shows in detail the entire process of creating a fractal.

⇡ XaoS: fractals for every taste

Many graphic editors have built-in tools for creating fractal patterns. However, these tools are usually secondary and do not allow fine tuning of the generated fractal pattern. In cases where it is necessary to construct a mathematically accurate fractal, the cross-platform editor XaoS will come to the rescue. This program makes it possible not only to construct a self-similar image, but also to perform various manipulations with it. For example, in real time you can take a “walk” along a fractal by changing its scale. Animated movement along a fractal can be saved as an XAF file and then reproduced in the program itself.

XaoS can load a random set of parameters, and also use various image post-processing filters - add a blurred motion effect, smooth out sharp transitions between fractal points, simulate a 3D image, and so on.

⇡ Fractal Zoomer: compact fractal generator

Compared to other fractal image generators, it has several advantages. Firstly, it is very small in size and does not require installation. Secondly, it implements the ability to determine the color palette of a picture. You can choose shades in RGB, CMYK, HVS and HSL color models.

It is also very convenient to use the option of randomly selecting color shades and the function of inverting all colors in the picture. To adjust the color, there is a function of cyclical selection of shades - when you turn on the corresponding mode, the program animates the image, cyclically changing the colors on it.

Fractal Zoomer can visualize 85 different fractal functions, and the formulas are clearly shown in the program menu. There are filters for image post-processing in the program, although in small quantities. Each assigned filter can be canceled at any time.

⇡ Mandelbulb3D: 3D fractal editor

When the term "fractal" is used, it most often refers to a flat, two-dimensional image. However, fractal geometry goes beyond the 2D dimension. In nature, you can find both examples of flat fractal forms, say, the geometry of lightning, and three-dimensional volumetric figures. Fractal surfaces can be three-dimensional, and one very clear illustration of 3D fractals in everyday life is a head of cabbage. Perhaps the best way to see fractals is in the Romanesco variety, a hybrid of cauliflower and broccoli.

You can also eat this fractal

The Mandelbulb3D program can create three-dimensional objects with a similar shape. To obtain a 3D surface using a fractal algorithm, the authors of this application, Daniel White and Paul Nylander, converted the Mandelbrot set to spherical coordinates. The Mandelbulb3D program they created is a real three-dimensional editor that models fractal surfaces of different shapes. Since we often observe fractal patterns in nature, an artificially created fractal three-dimensional object seems incredibly realistic and even “alive.”

It may resemble a plant, it may resemble a strange animal, a planet, or something else. This effect is enhanced by an advanced rendering algorithm, which makes it possible to obtain realistic reflections, calculate transparency and shadows, simulate the effect of depth of field, and so on. Mandelbulb3D has a huge number of settings and rendering options. You can control the shades of light sources, select the background and level of detail of the simulated object.

The Incendia fractal editor supports double image smoothing, contains a library of fifty different three-dimensional fractals, and has a separate module for editing basic shapes.

The application uses fractal scripting, with which you can independently describe new types of fractal designs. Incendia has texture and material editors, and the rendering engine allows you to use volumetric fog effects and various shaders. The program implements the option of saving a buffer during long-term rendering, and supports the creation of animation.

Incendia allows you to export a fractal model to popular 3D graphics formats - OBJ and STL. Incendia includes a small utility called Geometrica, a special tool for setting up the export of a fractal surface to a 3D model. Using this utility, you can determine the resolution of a 3D surface and specify the number of fractal iterations. Exported models can be used in 3D projects when working with 3D editors such as Blender, 3ds max and others.

Recently, work on the Incendia project has slowed down somewhat. At the moment, the author is looking for sponsors to help him develop the program.

If you don’t have enough imagination to draw a beautiful three-dimensional fractal in this program, it doesn’t matter. Use the parameters library, which is located in the INCENDIA_EX\parameters folder. Using PAR files, you can quickly find the most unusual fractal shapes, including animated ones.

⇡ Aural: how fractals sing

We usually don’t talk about projects that are just being worked on, but in this case we have to make an exception, since this is a very unusual application. The project, called Aural, was invented by the same person who created Incendia. However, this time the program does not visualize the fractal set, but sounds it, turning it into electronic music. The idea is very interesting, especially considering the unusual properties of fractals. Aural is an audio editor that generates melodies using fractal algorithms, that is, in essence, it is an audio synthesizer-sequencer.

The sequence of sounds produced by this program is unusual and... beautiful. It may well be useful for writing modern rhythms and, it seems to us, is especially well suited for creating soundtracks for screensavers of television and radio programs, as well as “loops” of background music for computer games. Ramiro has not yet provided a demo of his program, but promises that when he does, in order to work with Aural, you will not need to study fractal theory - you will just need to play with the parameters of the algorithm for generating a sequence of notes. Listen to how fractals sound, and.

Fractals: musical break

In fact, fractals can help you write music even without software. But this can only be done by someone who is truly imbued with the idea of ​​natural harmony and who has not turned into an unfortunate “nerd.” It makes sense to take an example from a musician named Jonathan Coulton, who, among other things, writes compositions for Popular Science magazine. And unlike other performers, Colton publishes all of his works under a Creative Commons Attribution-Noncommercial license, which (when used for non-commercial purposes) provides for free copying, distribution, transfer of the work to others, as well as its modification (creation of derivative works) so that adapt it to your tasks.

Jonathan Colton, of course, has a song about fractals.

⇡ Conclusion

In everything that surrounds us, we often see chaos, but in fact this is not an accident, but an ideal form, which fractals help us to discern. Nature is the best architect, ideal builder and engineer. It is structured very logically, and if we don’t see a pattern somewhere, this means that we need to look for it on a different scale. People understand this better and better, trying to imitate natural forms in many ways. Engineers design shell-shaped speaker systems, create snowflake-shaped antennas, and so on. We are sure that fractals still contain many secrets, and many of them have yet to be discovered by humans.