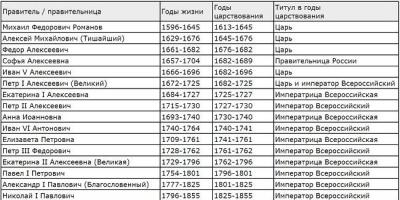
Fundamental concepts of chemical thermodynamics are applicable to the characterization of phase equilibrium and phase transitions.
Phase balance means the simultaneous existence of thermodynamically equilibrium phases in a heterogeneous system.
For example, a liquid with its saturated vapor (liquid-gas system), water and ice at a melting point (liquid-solid system), two immiscible liquids (liquid-liquid system), etc.
The phase equilibrium depending on the composition and parameters of the system is determined by the Gibbs phase rule.
System
/ \
homogeneous(single phase) heterogeneous(polyphase)
Phase- a homogeneous part of a heterogeneous system that has a certain set of physical and chemical properties and is separated from other phases by an interface.
Component- a part of a system that can be isolated from it and exist outside of this system.
For example, NaCl solution: NaCl components and water.
The number of independent components (parameters) is equal to the total number of components (parameters) minus the number of equations connecting them.
Phase transitions.
1) crystallization(∆H<0)
2) melting(∆H>0)
3) evaporation(∆H>0)
4) condensation(∆H<0)
5) sublimation (sublimation)(∆H>0)
6) desublimation(∆H<0)
Equilibrium conditions in a heterogeneous system.
Possibility T 1 ≠T 2 
Direction T 1 > →T 2< 
Limit T 1 =T 2 T,P– intensity factors
To determine the possibility, direction and limit of processes in heterogeneous systems, one can use the expression  (µ
i
– chemical potential) – intensity factor phase transition.
(µ
i
– chemical potential) – intensity factor phase transition.
In the figure, we present the transition scheme of a certain small amount of the component i from phase I to phase II.

µ i I >µ i II
The possibility of a phase transition is determined by the chemical potential.
1) Process capability: µ i I ≠ µ i II
2) Process direction: If µ i I >µ i II , That I→II
3) Process limit:µ i I = µ i II
If, for example, a liquid is in equilibrium with its vapor, then the chemical potential is the same for vapor and liquid ( µ i and = µ i P). As the temperature rises, the chemical potential of the component in the gas medium decreases and becomes lower than its chemical potential in the liquid medium. Then, in accordance with the condition µ i and > µ i P part of the liquid will spontaneously evaporate until the chemical potentials of the conjugated phases are equalized.
The effect of external parameters on phase equilibrium and phase transitions is determined by Gibbs phase rule.
Gibbs phase rule.
CONCLUSION AND ANALYSIS.
To express the composition of a two-component system, it is sufficient to know the proportion of one component in the system, while the content of the second component will be quite definite.
For a system that includes two or more components, you can limit yourself to the content (K-1) of the components. If, for example, a glass of tea contains 3 components (water, tea, sugar), and sugar contains 0.7%, tea 0.3%, then it is natural that the rest falls on water, that is, it is enough to know the content of two components - on one less system composition.
When distributing these components in F phases, F(K-1) data will be required to describe the composition of the system. When the composition of the system changes depending on external parameters (eg, temperature, pressure), the number of which is n, the total number of data on the composition of the system is F(K-1)+n.
NUMBER OF EQUATIONS RELATED TO THE EQUILIBRIUM STATE OF K-COMPONENTS IN F-PHASES.
Let me remind you that the equilibrium state is characterized by the absence of changes in the Gibbs energy or Helmholtz energy ΔG=0 or ΔF=0.
The condition for the equilibrium of phases in a heterogeneous multicomponent system is the equality of the chemical potentials of any component in all phases. Then the number of equations relating the equilibrium state of the K components in the F phases is:
Total (F-1) equations
 …………………….. (F-1) equations
…………………….. (F-1) equations
 …………………….. (F-1) equations
…………………….. (F-1) equations
To characterize the phase state of the system, the concept of the number of degrees of freedom is introduced.
Number of degrees of freedom equilibrium thermodynamic system is the number of parameters (for example, temperature, pressure, concentration for a multicomponent system) that can be arbitrarily changed without changing the number and type of phases.
The number of degrees of freedom is denoted by C.
Let me remind you that the total number of system parameters is expressed as Ф(К-1)+n. But not all components Ф(К-1)+n, which determine the composition of the system, are independent of each other. The number of degrees of freedom C is equal to the total number of data on the composition of the system minus the number of bonds between them K(F-1):
S \u003d F (K-1) + n-K (F-1) or
C = K – F+n*
Within the Earth, all systems are in the same conditions, and the effects of gravitational, magnetic, electric and other fields can be ignored. Among the external parameters taken into account for condensed systems (liquid, solid) are temperature, n=1, and for non-condensed systems (gas), also pressure, i.e. n=2. Thus, the equation * C \u003d K – Ф + n takes the form:
C \u003d K-F + 1 ** C \u003d K-F + 2 ***
All three equations express Gibbs phase rule, which is formulated as follows:
The number of degrees of freedom of an equilibrium thermodynamic system affected bynexternal factors is equal to the number of independent system components minus the number of phases plusn.
C is the number of degrees of freedom.
K is the number of independent components.
Ф is the number of phases of the system.
n is the number of external parameters affecting the system.
n=2 (T, P) ;n=1 (T or P)
A substance can change from one state of aggregation to another when changing pressure and temperature. These transitions, which take place at a constant temperature, are called first-order phase transitions. The amount of heat that a substance receives from the environment or gives off to the environment during a phase transition is the latent heat of the phase transition lfp. If a heterogeneous system is considered in which there are no chemical interactions, but only phase transitions are possible, then at a constant temperature and pressure in the system there is a so-called. phase balance. Phase equilibrium is characterized by a certain number of phases, components, and the number of degrees of thermodynamic freedom of the system.
A component is a chemically homogeneous component of a system that can be isolated from the system and exist outside of it. The number of independent components of the system is equal to the number of components minus the number of possible chemical reactions between them.
The number of degrees of freedom is the number of system state parameters that can be simultaneously arbitrarily changed within certain limits without changing the number and nature of phases in the system.
The number of degrees of freedom of a heterogeneous thermodynamic system in a state of phase equilibrium is determined by the phase rule formulated by J. Gibbs:
The number of degrees of freedom of an equilibrium thermodynamic system C is equal to the number of independent components of the system K minus the number of phases Ф plus the number of external factors affecting the equilibrium.
For a system that is affected only by temperature and pressure among external factors, we can write:
C \u003d K - F + 2 (I.108)
Systems are usually classified according to the number of components (one-, two-component, etc.), the number of phases (one-, two-phase, etc.) and the number of degrees of freedom (invariant, mono-, divariant, etc.). For systems with phase transitions, a graphical dependence of the state of the system on external conditions is usually considered - the so-called. state diagrams.
The analysis of state diagrams makes it possible to determine the number of phases in the system, the boundaries of their existence, and the nature of the interaction of components. The analysis of state diagrams is based on two principles: the principle of continuity and the principle of correspondence. According to the principle of continuity, with a continuous change in state parameters, all properties of individual phases also change continuously; the properties of the system as a whole change continuously until the number or nature of the phases in the system changes, which leads to an abrupt change in the properties of the system. According to the correspondence principle, on the system state diagram, each phase corresponds to a part of the plane - the phase field. The lines of intersection of the planes correspond to the equilibrium between the two phases. Any point on the state diagram (the so-called figurative point) corresponds to a certain state of the system with certain values of the state parameters.
Consider and analyze the state diagram of water (Fig. 1.4). Since water is the only substance present in the system, the number of independent components is K = 1. Three phase equilibria are possible in the system: between liquid and gas (line OA - dependence of saturated water vapor pressure on temperature), solid body and gas (line OB - pressure dependence saturated vapor over ice on temperature), solid and liquid (line OS - dependence of the melting temperature of ice on pressure). The three curves have a point of intersection O, called the triple point of water; the triple point corresponds to the equilibrium between the three phases.
Rice. 1.4.
At the triple point, the system is three-phase and the number of degrees of freedom is zero; the three phases can be in equilibrium only at strictly defined values of temperature and pressure (for water, the triple point corresponds to the state with P = 6.1 kPa and T = 273.16 K).
The RH curve theoretically continues to absolute zero, and the saturated vapor pressure curve over the OA liquid ends at the critical point of water (Tcr = 607.46 K, Pcr = 19.5 MPa); above the critical temperature, gas and liquid cannot exist as separate phases. The OS curve in the upper part (at high pressures) changes its slope (new crystalline phases appear, the density of which, unlike ordinary ice, is higher than that of water).
Inside each of the areas of the diagram (AOB, VOS, AOS), the system is single-phase; the number of degrees of freedom of the system is two (the system is divariant), i.e. it is possible to simultaneously change both temperature and pressure without causing a change in the number of phases in the system:
C \u003d 1 - 1 + 2 \u003d 2
On each of the lines, the number of phases in the system is equal to two and, according to the phase rule, the system is monovariant, i.e. for each temperature value, there is only one pressure value at which the system is two-phase:
C \u003d 1 - 2 + 2 \u003d 1
The effect of pressure on the phase transition temperature is described by the Clausius-Clapeyron equation:
Here DVfp = V2 - V1 is the change in the molar volume of the substance during the phase transition (moreover, V2 refers to the state, the transition to which is accompanied by the absorption of heat). The Clausius-Clapeyron equation makes it possible to explain the slope of the equilibrium curves in the state diagram of a one-component system. For transitions "liquid - vapor" and "solid matter - vapor" DV is always greater than zero; therefore, the phase diagram curves corresponding to these equilibria always slope to the right (an increase in temperature always increases the saturation vapor pressure). Since the molar volume of a gas is much greater than the molar volume of the same substance in a liquid or solid state of aggregation (Vg >> Vl, Vg >> Vt), equation (I.109) for special cases of evaporation and sublimation will take the following form:
For many substances, the latent heat of vaporization or sublimation is constant over a wide temperature range; in this case equation (I.110) can be integrated:

The equilibrium curve "solid matter - liquid" on the state diagrams of water and bismuth is inclined to the left, and on the state diagrams of other substances - to the right. This is due to the fact that the density of water is greater than the density of ice (and the density of liquid bismuth is greater than its density in the solid state), i.e. melting is accompanied by a decrease in volume (ДV< 0). Как следует из выражения (I.111), в этом случае увеличение давления будет понижать температуру фазового перехода "твердое тело - жидкость" (воду и висмут относят поэтому к т.н. аномальным веществам). Для всех остальных веществ (т.н. нормальные вещества) ДVпл >0 and, according to the Clausius-Clapeyron equation, an increase in pressure leads to an increase in the melting point.
The method of determining the equilibrium constants according to the NGAA atlas issued by the American Gasoline Production Association has received the greatest distribution both in our country and abroad. The atlas contains equilibrium constants from methane to decane inclusive, as well as nitrogen and carbon dioxide. The equilibrium constant at a given convergence pressure is determined from an atlas based on pressure and temperature data. When calculating on a computer, it is difficult to use graphs of equilibrium constants, because one has to repeatedly remove the values of the constants from the graphs and enter them into the computer memory. In this regard, the NGAA atlases are translated into tables:
Recommendations for automating the choice of equilibrium constants of hydrocarbon systems on a computer. Tables of equilibrium constants. All-Russian Research Institute of Gas, Moscow, 1972. A partial atlas of equilibrium constants is presented in the reference book: Katz, "Gas Production and Transportation".
Phase equilibrium equations.
For calculations, the following initial data are needed:
Initial reservoir pressure
Initial formation temperature
Composition of the hydrocarbon system
Equilibrium constants of individual constituent components, K=y/x, where
y is the molar fraction of the component in the gas phase,
x-molar fraction of a component in the liquid phase in equilibrium with the gas phase.
Each component of the mixture at a given temperature and pressure has its own equilibrium constants. They are determined experimentally. Dependences of the equilibrium constant are expressed in terms of the given parameters:
, , ![]() .
.
In the case of a multicomponent mixture, the critical pressure is called the convergence pressure. Since there is no difference between liquid and vapor (gas) in the critical and supercritical regions, then for a mixture:
![]()
The convergence pressure corresponds to a certain composition of the mixture and is a numerical characteristic of the composition.
The atlas of constants was compiled for a wide range of changes in P cx.
For a multicomponent mixture, an equation of phase concentrations is compiled. N is the mass of all components in a certain volume V. N G is the mass of components in a gas, N W is the mass of components in a liquid N = N G +N L.
If we divide by the sum of the molecular weights of all components contained in the volume V, we get n M = n MG + n MF is the number of moles of the components in the gas and liquid phases.
Mole fraction of components in gas "y i" and in liquid "x i":


N G i - mass of the i-th component in the gas phase
N w i is the mass of the i-th component in the liquid phase
M i - molecular weight of the i-th component
The molar fraction of the i-th component in the volume as a whole is expressed:

N i is the mass of the i-th component in the volume V.
From the above expressions it follows: ![]() (*)
(*)
Denote:
n MG / n M = Y is the mole fraction of all components in the gas phase.
n MF / n M \u003d X is the mole fraction of all components in the liquid phase
Considering y i = K i x i ? 1=X+Y, substitute into equality (*)
![]() ,
, ![]() Equations of phase concentrations
Equations of phase concentrations
When determining the phase state, various problems can be solved.
For example, given: ν i (composition), P,T,Y → then determine x i and y i from ur-th concentrations. More often there is a problem of finding Y,X according to the known composition ν i , P,T. Then the equality is used ![]() . The equation is solved by an iterative method. The original equation is solved in the form:
. The equation is solved by an iterative method. The original equation is solved in the form: ![]() .
.
It is obvious that for Y=0 f(Y)=0.
The maximum value of the proportion of the gas phase Y=1. hence the solution is sought in the interval 0
Taking as the initial approximation Y 0 =0.5 and applying sequentially the iterative formulas of the Newton method - the method of chords, a solution is found with a small number of iterations:
![]()
![]()
Two-phase filtration.
In connection with the design and analysis of the development of oil and gas fields, it is necessary to study the joint flow in a porous medium of several liquids, most often water, oil and gas, which are separate phases that do not mix with each other.
The formation of deposits occurs as a result of the displacement of the water that was originally there. Therefore, along with oil and gas in the reservoirs there is a certain amount (10-30%) of buried water. In addition, many deposits are filled with oil and gas only in the upper dome part, while the underlying zones are filled with water with its initial content that was not pushed aside during the formation process. The uppermost parts of the reservoir contain gas that may be present or collected during development. A two- or three-phase flow occurs during the development of oil deposits, oil and gas, gas condensate, and simply gas deposits in the presence of water underlying the gas cap, i.e. almost always, except for dry gas traps.
When filtering two liquids (oil-water), or liquid and gas (oil-gas, water-gas), Darcy's law has a different form than with a single-phase function:
![]() ,
, ![]()
Here K 1 (S)? K 2 (S) - relatively phase permeability, depending on S - saturation of the 2nd phase, usually water, 1st phase - oil and gas.
In hydrodynamic calculations, it is often convenient to use empirical dependences of relative phase permeability on saturation obtained from experimental data. Let's consider the empirical formulas obtained by Chen-Zhong-Xiang, which can be used in estimating calculations.
1. For water and oil (s-water saturation):
![]()
2. for gas and water (s-gas saturation):

The behavior of relative phase permeabilities is described by graphs of the form:
Dependencies have two characteristic points S st, S *
At the point S \u003d Sv relative water permeability \u003d 0 \u003d K 2 (S)
At point S=S * relative permeability of oil (gas) = 0
At these points, the phase with zero permeability is dispersed and occupies isolated dead ends in a porous medium, and therefore is not mobile. Simultaneous filtration of 3 phases has been studied less than two-phase. Use this approach. S n + S in \u003d S well, considering 2 phases - liquid and gas S G + S well \u003d 1 two-phase system.
![]() two-phase system, K n (S), K in (S)
two-phase system, K n (S), K in (S)
K G (S f), K f (S f)
All relative permeabilities are determined from two-phase diagrams, (S G, S W) and ![]()
Then the relative permeability for oil is K f (S f) K n (S)
for water - K w (S w) K in (S)
for gas - K G (S well)
![]()
![]()
![]()
For thick seams, or sloping seams, where gravity must be taken into account, if the Z axis, then the vertical component of the two-three-phase filtration rate instead contains:
 P are the same pressures in the phases.
P are the same pressures in the phases.
P * = P + ρgZ reduced pressures.
We have considered expressions for the filtration rate for two, three-phase filtration flow. If two or three immiscible phases (oil, gas, water) are moving, then the same type of equations will be written for each separately:

I=1, 2, 3 where 1 is gas
2 - oil
3 - water or:
The difference from the equation of continuity of a single-phase liquid - the equation includes - the saturation of the phases. On the left side, S i affect the phase permeabilities. On the right side, when compiling the mass balance for an element, we must take into account for a separate phase not the entire pore volume, but its share occupied by the i-th phase.
If we substitute expressions for velocities as functions of pressure and saturation into the system of equations for the continuity of phases, as well as expressions for phase densities as functions of pressure, then for a system of 3 equations we have unknowns 4-P, S 1, S 2 , S 3.
The system is closed by the relation: S 1 + S 2 + S 3 = 1.
In this case, it was assumed that the pressures in the phases are the same Р.
capillary forces. Interfacial (capillary) pressure forces arise in pore channels, for example, in a two-phase flow.

R g - R f = R k (S f)
Since the functions P k (S w) have been studied experimentally, the input cap. forces in the equation does not add the number of unknowns.
7. Multi-phase multi-component filtration. Three-phase - two-three-dimensional filtration.
We consider a system from " nl" phases, for example:
1st phase - oil wetting by gas, non-wetting by water;
2nd phase - water, wetting;
3rd phase - gas, non-wetting.
In general, the system consists of nc"chemical components. When moving, changing the pressure, temperature of the mixture, individual hydrocarbon components can transfer from the oil phase to the gas phase and vice versa. The transition of water into a gaseous state is not excluded during thermal action on the formation. Mass transfer between the phases occurs by various components. In this case, the material the balance when deriving the continuity equation is written for each component separately, and as a result we have " nc"continuity equations.
Fraction of the pore space of the mesh element occupied by " 1 "th phase - S 1 ;
C e j - concentration j- th component in 1 is the phase in the grid volume under consideration.
Then the change in mass j- th component in the grid element must be considered as the sum of its changes in each phase, taking into account ( S 1 C e j) – fraction of the pore volume of the element occupied j- component in 1 – oh phase;
S l C lj ρ l- mass fraction j- 1 – oh phase;
Total mass fraction j- th component in the pore volume of the grid element 1 – oh phase;
![]() - mass fraction j- th component in the pore volume of the grid element;
- mass fraction j- th component in the pore volume of the grid element;
Ω el is the volume of the grid element.
Mass change j- th component in a short period of time Δt, in the case of a Cartesian coordinate system, we write the form:
Let be the density of the source (sink) 1 – oh phase, - concentration j- th component in the source 1 - oh phase.
Then - the total density of the source according to j- oh component.
The flow terms in the continuity equation, in contrast to the single-phase motion, contain
Bulk speed j- th component in the stream 1 - oh phase.
In the material balance equation j- th component, the flows of the considered component over all phases are summed up.
As a result, the continuity equation for j- th component looks like:
The number of system equations is determined by the number of moving components j=1,2,…,n c .
Three-phase model of an oil reservoir.
In the design of oil reservoirs, the non-volatile oil model (beta model) has been widely used. The hydrocarbon system is approximated by two components: non-volatile (oil) and volatile (gas) soluble in oil. It is assumed that three separate phases coexist in a porous medium: oil, gas, and water.
Water and oil do not mix, do not exchange masses and do not change phases.
The gas is soluble in oil, insoluble in water.
Fluids are assumed to be in thermodynamic equilibrium at constant temperature.
Consider the movement of a three-phase fluid: oil, gas, water (g, o, c):
the gas phase consists of one component - free gas;
water phase - from one water component;
oil phase - 2-component, oil and gas dissolved in it.
Let us determine the concentrations of the components in the phase; 1,2 - oil, gas.
C H1 is the concentration of oil in the oil phase;
C H2 - gas concentration in the oil phase;
C B1 \u003d C B2 \u003d 0, i.e. the water phase does not contain a component of gas and oil;
C G2 = 1, i.e. the gas phase contains only gas;
WITH lj– mass concentration j- th component in 1 - oh phase.
Consider the left side of the equation for the continuity of a multiphase fluid.
![]() (sums for all phases of flows j- th component).
(sums for all phases of flows j- th component).
Let us introduce the concept of volumetric phase coefficients: the ratio of the phase volume in reservoir conditions to the volume in standard conditions.
For the gas phase:
For the aqueous phase:
For the oil phase:
here - the volume of oil in reservoir conditions, taking into account the gas dissolved in it;
 .
.
Main literature
additional literature
1. Lysenko VD Innovative development of oil fields. - M.: Nedra-Business Center, 2000. - 516s. - Bibliography: pp.513-514
2. Zakirov, S. N. Development of gas, gas condensate and oil and gas condensate fields / S.N. Zakirov. - M. : Struna, 1998. - 626 p. - Bibliography: p. 597-620. - ISBN 5-85926-011-3
3. Zheltov, Yu. P. Development of oil fields: a textbook for universities / Yu. P. Zheltov. - 2nd ed., revised. and additional - M. : Nedra, 1998. - 365 p. : ill. - Bibliography. With. 359. - ISBN 5-247-03806-1
4. Kanevskaya R.D. Mathematical modeling of hydrodynamic processes in the development of hydrocarbon deposits. - M. - Izhevsk: Institute of Computer Research, 2002. - 140 p.
Heterogeneous equilibria associated with the transition of a substance from one phase to another without changing the chemical composition are called phase. These include equilibria in the processes
evaporation, melting, condensation, etc. Phase equilibria, like chemical ones, are characterized by the minimum value of the Gibbs energy of the system and the equality of the rates of the direct and reverse processes. So, for example, the equilibrium in the ice-water system is characterized by the equality of the rates of ice melting and water crystallization.
For phase equilibria, Le Chatelier's principle is valid. In the ice-water system, the equilibrium can be shifted to the right side (towards the melting of ice) by increasing the temperature, since the transition is accompanied by the absorption of energy, and in the steam-water system: when the temperature rises, the equilibrium shifts to the left (toward the evaporation of water), since the process is accompanied by the absorption of energy
One of the most general laws of heterogeneous (including phase) equilibria is the phase rule. According to this rule, in an equilibrium system, the number of phases F, the number of independent components K, and the number of degrees of freedom C are related by the relation:
![]()
where is the number of external factors affecting the equilibrium of the system.
Until now, the concept of "component" has been used to refer to any substance that is an integral part of the system. For example, in an aqueous solution of copper sulfate, the components are Now we introduce the concept of "independent component". The number of independent components K in the system is the smallest number of its components sufficient to form all phases of the given system. When considering phase equilibria, when no chemical transformations occur in the system, the concepts of “component” and “independent component” coincide. But if a chemical reaction takes place in the system, these concepts are different. In chemical equilibrium, the relative amounts of all substances in the system are mutually related. So, there are three components in the system, but only two are independent, since at equilibrium the content of any of the three components is uniquely determined by the content of the other two:
![]()
where is the equilibrium constant.
In the general case, the number of independent components K is equal to

Rice. V.10. state diagram
the total number of components minus the number of equations of independent reactions connecting these components.
External factors affecting the equilibrium of the system are most often temperature and pressure. Then equation (V.35) also takes the form
![]()
The number of degrees of freedom (more precisely, thermodynamic degrees of freedom) C is equal to the number of conditions (temperature, pressure, concentration), an arbitrary change of which, within certain limits, does not change the number and type of phases of the system. According to the number of degrees of freedom, systems are divided into invariant monovariant bivariant and polyvariant
Consider a one-component system According to equation (V.36), at Since the number of degrees of freedom cannot be negative, the number of phases of a one-component system that are in equilibrium with each other cannot be more than three. One-component systems can be single-phase, two-phase and three-phase.
In the study of phase equilibria, the graphical method is widely used - the method of constructing state diagrams. A state diagram can be built on the basis of experimental data for any substance; it allows one to judge the stability of any one phase of the system and the stability of the equilibrium between two or three phases under given conditions. On fig. V.10 shows a phase diagram of silver iodide having three crystalline modifications: A, B and C. Each modification, i.e. each phase, corresponds to a certain area of the diagram, separated from other areas by lines characterizing the equilibrium between two separate phases. So, for example, the line characterizes the balance between crystalline modifications A and B.
Within each area of the diagram (A, B and C) the system is single-phase and the number of degrees of freedom is two. This means that both temperature and pressure can be changed within certain limits without any change in the number or type of phases. Thus, at any pressure within the range and at any temperature within the range, crystal modification A is stable, and under conditions, modification B.
Each curve in the diagram refers to a two-phase system. The number of degrees of freedom corresponding to the equilibrium of two phases is equal to one. This means that
that only the temperature (or only the pressure) can be changed arbitrarily. The system is monovariant. For example, crystalline forms of silver iodide A and B can be in equilibrium at different temperatures and pressures (curve 1), but each pressure corresponds to a strictly defined temperature and, conversely, to each temperature, a strictly defined pressure. So, the equilibrium A at corresponds to
A point on a state diagram is called a triple point. It intersects all three curves. This point corresponds to the equilibrium between three phases: A, B and C. The number of degrees of freedom of an equilibrium three-phase system is equal to zero. The system is invariant. The equilibrium conditions (temperature and pressure) are strictly defined, and none of them can change.
Often, in one-component systems, individual phases are the same substance in various states of aggregation - solid, liquid and gaseous. Each state of aggregation, i.e., each phase, corresponds to a certain area of the diagram of the state of matter. Boundary lines characterize the equilibrium: a) between the gaseous and liquid phases, b) between the liquid and solid phases, c) between the solid and gaseous phases. The triple point shows the values of temperature and pressure at which all three phases coexist, that is, the substance in all three states of aggregation.