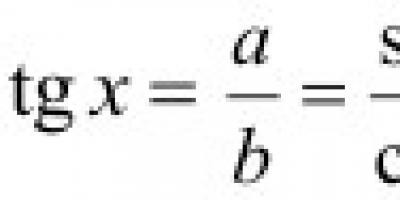Trigonometry is simple and clear. Trigonometry from scratch: basic concepts, history Everything you need to know about trigonometry

The video course “Get an A” includes all the topics necessary to successfully pass the Unified State Exam in mathematics with 60-65 points. Completely all tasks 1-13 of the Profile Unified State Exam in mathematics. Also suitable for passing the Basic Unified State Examination in mathematics. If you want to pass the Unified State Exam with 90-100 points, you need to solve part 1 in 30 minutes and without mistakes!

Preparation course for the Unified State Exam for grades 10-11, as well as for teachers. Everything you need to solve Part 1 of the Unified State Exam in mathematics (the first 12 problems) and Problem 13 (trigonometry). And this is more than 70 points on the Unified State Exam, and neither a 100-point student nor a humanities student can do without them.

All the necessary theory. Quick solutions, pitfalls and secrets of the Unified State Exam. All current tasks of part 1 from the FIPI Task Bank have been analyzed. The course fully complies with the requirements of the Unified State Exam 2018.

The course contains 5 large topics, 2.5 hours each. Each topic is given from scratch, simply and clearly.

Hundreds of Unified State Exam tasks. Word problems and probability theory. Simple and easy to remember algorithms for solving problems. Geometry. Theory, reference material, analysis of all types of Unified State Examination tasks. Stereometry. Tricky solutions, useful cheat sheets, development of spatial imagination. Trigonometry from scratch to problem 13. Understanding instead of cramming. Clear explanations of complex concepts. Algebra. Roots, powers and logarithms, function and derivative. A basis for solving complex problems of Part 2 of the Unified State Exam.

When performing trigonometric conversions, follow these tips:

1. Don't try to immediately come up with a solution to the example from start to finish.
2. Don't try to convert the entire example at once. Take small steps forward.
3. Remember that in addition to trigonometric formulas in trigonometry, you can still use all fair algebraic transformations (bracketing, abbreviating fractions, abbreviated multiplication formulas, and so on).
4. Believe that everything will be fine.

Basic trigonometric formulas

Most formulas in trigonometry are often used both from right to left and from left to right, so you need to learn these formulas so well that you can easily apply some formula in both directions. Let us first write down the definitions of trigonometric functions. Let there be a right triangle:

Then, the definition of sine:

Definition of cosine:

Tangent definition:

Definition of cotangent:

Basic trigonometric identity:

The simplest corollaries from the basic trigonometric identity:

Double angle formulas. Sine of double angle:

Cosine of double angle:

Tangent of double angle:

Cotangent of double angle:

Additional trigonometric formulas

Trigonometric addition formulas. Sine of the sum:

Sine of the difference:

Cosine of the sum:

Cosine of the difference:

Tangent of the sum:

Tangent of difference:

Cotangent of the amount:

Cotangent of the difference:

Trigonometric formulas for converting a sum into a product. Sum of sines:

Sine difference:

Sum of cosines:

Difference of cosines:

Sum of tangents:

Tangent difference:

Sum of cotangents:

Cotangent difference:

Trigonometric formulas for converting a product into a sum. Product of sines:

Product of sine and cosine:

Product of cosines:

Degree reduction formulas.

Half angle formulas.

Trigonometric reduction formulas

The cosine function is called cofunction sine functions and vice versa. Similarly, the tangent and cotangent functions are cofunctions. Reduction formulas can be formulated as the following rule:

• If in the reduction formula an angle is subtracted (added) from 90 degrees or 270 degrees, then the reduced function changes to a cofunction;
• If in the reduction formula the angle is subtracted (added) from 180 degrees or 360 degrees, then the name of the reduced function is retained;
• In this case, the sign that the reduced (i.e., original) function has in the corresponding quadrant is placed in front of the reduced function, if we consider the subtracted (added) angle to be acute.

Reduction formulas are given in table form:

By trigonometric circle easy to determine tabular values ​​of trigonometric functions:

Trigonometric equations

To solve a certain trigonometric equation, it must be reduced to one of the simplest trigonometric equations, which will be discussed below. For this:

• You can use the trigonometric formulas given above. At the same time, you don’t need to try to transform the entire example at once, but you need to move forward in small steps.
• We must not forget about the possibility of transforming some expression using algebraic methods, i.e. for example, take something out of brackets or, conversely, open brackets, reduce a fraction, apply an abbreviated multiplication formula, bring fractions to a common denominator, and so on.
• When solving trigonometric equations, you can use grouping method. It must be remembered that in order for the product of several factors to be equal to zero, it is sufficient that any of them be equal to zero, and the rest existed.
• Applying variable replacement method, as usual, the equation after introducing the replacement should become simpler and not contain the original variable. You also need to remember to perform a reverse replacement.
• Remember that homogeneous equations often appear in trigonometry.
• When opening modules or solving irrational equations with trigonometric functions, you need to remember and take into account all the subtleties of solving the corresponding equations with ordinary functions.
• Remember about ODZ (in trigonometric equations, restrictions on ODZ mainly come down to the fact that you cannot divide by zero, but do not forget about other restrictions, especially about the positivity of expressions in rational powers and under the roots of even powers). Also remember that the values ​​of sine and cosine can only lie in the range from minus one to plus one, inclusive.

The main thing is, if you don’t know what to do, do at least something, and the main thing is to use trigonometric formulas correctly. If what you get gets better and better, then continue the solution, and if it gets worse, then go back to the beginning and try to apply other formulas, do this until you come across the correct solution.

Formulas for solutions of the simplest trigonometric equations. For sine there are two equivalent forms of writing the solution:

For other trigonometric functions, the notation is unambiguous. For cosine:

For tangent:

For cotangent:

Solving trigonometric equations in some special cases:

Successful, diligent and responsible implementation of these three points will allow you to show an excellent result at the CT, the maximum of what you are capable of.

Found a mistake?

If you think you have found an error in the training materials, please write about it by email. You can also report an error on the social network (). In the letter, indicate the subject (physics or mathematics), the name or number of the topic or test, the number of the problem, or the place in the text (page) where, in your opinion, there is an error. Also describe what the suspected error is. Your letter will not go unnoticed, the error will either be corrected, or you will be explained why it is not an error.

Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.

Collection and use of personal information

Personal information refers to data that can be used to identify or contact a specific person.

You may be asked to provide your personal information at any time when you contact us.

Below are some examples of the types of personal information we may collect and how we may use such information.

What personal information do we collect:

• When you submit an application on the site, we may collect various information, including your name, phone number, email address, etc.

How we use your personal information:

• The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
• From time to time, we may use your personal information to send important notices and communications.
• We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
• If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.

Disclosure of information to third parties

We do not disclose the information received from you to third parties.

Exceptions:

• If necessary - in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government authorities in the territory of the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
• In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.

Protection of personal information

We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.

Respecting your privacy at the company level

To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.

Once upon a time at school there was a separate course for the study of trigonometry. The certificate included grades in three mathematical disciplines: algebra, geometry and trigonometry.

Then, as part of the school education reform, trigonometry ceased to exist as a separate subject. In a modern school, the first acquaintance with trigonometry occurs in the 8th grade geometry course. A more in-depth study of the subject continues in the 10th grade algebra course.

The definitions of sine, cosine, tangent and cotangent are first given in geometry through the relationship of the sides of a right triangle.

The acute angle in a right triangle is the ratio of the opposite side to the hypotenuse.

Cosine The acute angle in a right triangle is the ratio of the adjacent leg to the hypotenuse.

Tangent The acute angle in a right triangle is the ratio of the opposite side to the adjacent side.

Cotangent The acute angle in a right triangle is the ratio of the adjacent side to the opposite side.

These definitions only apply to acute angles (0º to 90°).

For example,

in triangle ABC, where ∠C=90°, BC is the leg opposite to angle A, AC is the leg adjacent to angle A, AB is the hypotenuse.

The 10th grade algebra course introduces the definitions of sine, cosine, tangent and cotangent for any angle (including negative).

Consider a circle of radius R with center at the origin - point O(0;0). Let us denote the point of intersection of the circle with the positive direction of the abscissa axis as P 0 .

In geometry, an angle is considered as a part of a plane bounded by two rays. With this definition, the angle varies from 0° to 180°.

In trigonometry, the angle is considered as the result of the rotation of the ray OP 0 around the starting point O.

At the same time, they agreed to consider turning the beam counterclockwise as a positive direction of traversal, and clockwise as negative (this agreement is associated with the true movement of the Sun around the Earth).

For example, when the ray OP 0 is rotated around point O by an angle α counterclockwise, point P 0 will go to point P α,

when turning by angle α clockwise - to point F.

With this definition, the angle can take any value.

If we continue to rotate the beam OP 0 counterclockwise, when turning through an angle α°+360°, α°+360°·2,...,α°+360°·n, where n is an integer (n∈Ζ), again let's get to point P α:

Angles are measured in degrees and radians.

1° is an angle equal to 1/180 of the degree measure of the developed angle.

1 radian is the central angle whose arc length is equal to the radius of the circle:

∠AOB=1 rad.

Radian symbols are not usually written. The degree designation cannot be omitted from the record.

For example,

Point P α , obtained from point P 0 by rotating ray OP 0 around point O by angle α counterclockwise, has coordinates P α (x;y).

Let us drop a perpendicular P α A from point P α to the abscissa axis.

In right triangle OP α A:

P α A - leg opposite to angle α,

OA - leg adjacent to angle α,

OP α is the hypotenuse.

P α A=y, OA=x, OP α =R.

By definition of sine, cosine, tangent and cotangent in a right triangle we have:

Thus, in the case of a circle with a center at the origin of arbitrary radius sine angle α is the ratio of the ordinate of point P α to the length of the radius.

Cosine angle α is the ratio of the abscissa of point P α to the length of the radius.

Tangent angle α is the ratio of the ordinate of a point P α to its abscissa.

Cotangent angle α is the ratio of the abscissa of point P α to its ordinate.

The values ​​of sine, cosine, tangent and cotangent depend only on the value of α and do not depend on the length of the radius R (this follows from the similarity of circles).

Therefore, it is convenient to choose R=1.

A circle with center at the origin and radius R=1 is called a unit circle.

Definitions

1) Sinus angle α is called the ordinate of point P α (x;y) of the unit circle:

2) Cosine angle α is called the abscissa of the point P α (x;y) of the unit circle:

3) Tangent angle α is the ratio of the ordinate of a point P α (x;y) to its abscissa, that is, the ratio of sinα to cosα (where cosα≠0):

4) Cotangent angle α is the ratio of the abscissa of a point P α (x;y) to its ordinate, that is, the ratio of cosα to sinα (where sinα≠0):

The definitions introduced in this way allow us to consider not only trigonometric functions of angles, but also trigonometric functions of numerical arguments (if we consider sinα, cosα, tanα and ctgα as the corresponding trigonometric functions of an angle in α radians, that is, the sine of the number α is the sine of the angle in α radians, the cosine of the number α is the cosine of the angle in α radians, etc.).

The properties of trigonometric functions are studied as a separate topic in the algebra course in grades 10 or 11. Trigonometric functions are widely used in physics.

In this lesson we will talk about how the need to introduce trigonometric functions arises and why they are studied, what you need to understand in this topic, and where you just need to get better at it (what is a technique). Note that technique and understanding are two different things. Agree, there is a difference: learning to ride a bicycle, that is, understanding how to do it, or becoming a professional cyclist. We will talk specifically about understanding, about why trigonometric functions are needed.

There are four trigonometric functions, but they can all be expressed in terms of one using identities (equalities that relate them).

Formal definitions of trigonometric functions for acute angles in right triangles (Fig. 1).

Sinus The acute angle of a right triangle is the ratio of the opposite side to the hypotenuse.

Cosine The acute angle of a right triangle is the ratio of the adjacent leg to the hypotenuse.

Tangent The acute angle of a right triangle is the ratio of the opposite side to the adjacent side.

Cotangent The acute angle of a right triangle is the ratio of the adjacent side to the opposite side.

Rice. 1. Determination of trigonometric functions of an acute angle of a right triangle

These definitions are formal. It is more correct to say that there is only one function, for example, sine. If they were not so needed (not so often used) in technology, so many different trigonometric functions would not be introduced.

For example, the cosine of an angle is equal to the sine of the same angle with the addition of (). In addition, the cosine of an angle can always be expressed through the sine of the same angle up to sign, using the basic trigonometric identity (). The tangent of an angle is the ratio of sine to cosine or an inverted cotangent (Fig. 2). Some don't use cotangent at all, replacing it with . Therefore, it is important to understand and be able to work with one trigonometric function.

Rice. 2. Relationship between various trigonometric functions

But why were such functions needed at all? What practical problems are they used to solve? Let's look at a few examples.

Two people ( A And IN) push the car out of the puddle (Fig. 3). Human IN can push the car sideways, but it is unlikely to help A. On the other hand, the direction of his efforts can gradually shift (Fig. 4).

Rice. 3. IN pushes the car sideways

Rice. 4. IN begins to change the direction of his efforts

It is clear that their efforts will be most effective when they push the car in one direction (Fig. 5).

Rice. 5. The most effective joint direction of effort

How much IN helps push the machine to the extent that the direction of its force is close to the direction of the force with which it acts A, is a function of the angle and is expressed through its cosine (Fig. 6).

Rice. 6. Cosine as a characteristic of effort efficiency IN

If we multiply the magnitude of the force with which IN, on the cosine of the angle, we obtain the projection of its force onto the direction of the force with which it acts A. The closer the angle between the directions of forces is to , the more effective the result of joint actions will be. A And IN(Fig. 7). If they push the car with the same force in opposite directions, the car will stay in place (Fig. 8).

Rice. 7. Effectiveness of joint efforts A And IN

Rice. 8. Opposite direction of forces A And IN

It's important to understand why we can replace an angle (its contribution to the final result) with a cosine (or other trigonometric function of an angle). In fact, this follows from this property of similar triangles. Since in fact we are saying the following: the angle can be replaced by the ratio of two numbers (side-hypotenuse or side-side). This would be impossible if, for example, for the same angle of different right triangles these ratios were different (Fig. 9).

Rice. 9. Equal side ratios in similar triangles

For example, if the ratio and ratio were different, then we would not be able to introduce the tangent function, since for the same angle in different right triangles the tangent would be different. But due to the fact that the ratios of the lengths of the legs of similar right triangles are the same, the value of the function will not depend on the triangle, which means that the acute angle and the values ​​of its trigonometric functions are one-to-one.

Suppose we know the height of a certain tree (Fig. 10). How to measure the height of a nearby building?

Rice. 10. Illustration of the condition of example 2

We find a point such that a line drawn through this point and the top of the house will pass through the top of the tree (Fig. 11).

Rice. 11. Illustration of the solution to the problem of example 2

We can measure the distance from this point to the tree, the distance from it to the house, and we know the height of the tree. From the proportion you can find the height of the house: .

Proportion is the equality of the ratio of two numbers. In this case, the equality of the ratio of the lengths of the legs of similar right triangles. Moreover, these ratios are equal to a certain measure of the angle, which is expressed through a trigonometric function (by definition, this is a tangent). We find that for each acute angle the value of its trigonometric function is unique. That is, sine, cosine, tangent, cotangent are really functions, since each acute angle corresponds to exactly one value of each of them. Consequently, they can be further explored and their properties used. The values ​​of trigonometric functions for all angles have already been calculated and can be used (they can be found from the Bradis tables or using any engineering calculator). But we cannot always solve the inverse problem (for example, using the value of the sine to restore the measure of the angle that corresponds to it).

Let the sine of some angle be equal to or approximately (Fig. 12). What angle will correspond to this sine value? Of course, we can again use the Bradis table and find some value, but it turns out that it will not be the only one (Fig. 13).

Rice. 12. Finding an angle by the value of its sine

Rice. 13. Polysemy of inverse trigonometric functions

Consequently, when reconstructing the value of the trigonometric function of an angle, the multivalued nature of the inverse trigonometric functions arises. This may seem difficult, but in reality we face similar situations every day.

If you curtain the windows and don’t know whether it’s light or dark outside, or if you find yourself in a cave, then when you wake up, it’s difficult to say whether it’s one o’clock in the afternoon, at night, or the next day (Fig. 14). In fact, if you ask us “What time is it?”, we must answer honestly: “Hour plus multiplied by where”

Rice. 14. Illustration of polysemy using the example of a clock

We can conclude that this is a period (the interval after which the clock will show the same time as now). Trigonometric functions also have periods: sine, cosine, etc. That is, their values ​​are repeated after some change in the argument.

If there was no change of day and night or change of seasons on the planet, then we could not use periodic time. After all, we only number the years in ascending order, but the days have hours, and every new day the counting begins anew. The situation is the same with months: if it is January now, then in a few months January will come again, etc. External reference points help us use periodic counting of time (hours, months), for example, the rotation of the Earth around its axis and the change in the position of the Sun and Moon in the sky. If the Sun always hung in the same position, then to calculate time we would count the number of seconds (minutes) from the moment this very calculation began. The date and time might then read like this: a billion seconds.

Conclusion: there are no difficulties in terms of polysemy of inverse functions. Indeed, there may be options when for the same sine there are different angle values ​​(Fig. 15).

Rice. 15. Restoring an angle from the value of its sine

Usually, when solving practical problems, we always work in the standard range from to . In this range, for each value of the trigonometric function there are only two corresponding values ​​of the angle measure.

Consider a moving belt and a pendulum in the form of a bucket with a hole from which sand pours out. The pendulum swings, the tape moves (Fig. 16). As a result, the sand will leave a trace in the form of a graph of the sine (or cosine) function, which is called a sine wave.

In fact, the graphs of sine and cosine differ from each other only in the reference point (if you draw one of them and then erase the coordinate axes, you will not be able to determine which graph was drawn). Therefore, there is no point in calling the cosine graph a graph (why come up with a separate name for the same graph)?

Rice. 16. Illustration of the problem statement in example 4

The graph of a function can also help you understand why inverse functions will have many values. If the value of the sine is fixed, i.e. draw a straight line parallel to the abscissa axis, then at the intersection we get all the points at which the sine of the angle is equal to the given one. It is clear that there will be an infinite number of such points. As in the example with the clock, where the time value differed by , only here the angle value will differ by the amount (Fig. 17).

Rice. 17. Illustration of polysemy for sine

If we consider the example of a clock, then the point (clockwise end) moves around the circle. Trigonometric functions can be defined in the same way - consider not the angles in a right triangle, but the angle between the radius of the circle and the positive direction of the axis. The number of circles that the point will go through (we agreed to count the movement clockwise with a minus sign, and counterclockwise with a plus sign), this is a period (Fig. 18).

Rice. 18. The value of sine on a circle

So, the inverse function is uniquely defined on a certain interval. For this interval, we can calculate its values, and get all the rest from the found values ​​by adding and subtracting the period of the function.

Let's look at another example of a period. The car is moving along the road. Let's imagine that her wheel has driven into paint or a puddle. Occasional marks from paint or puddles on the road may be seen (Figure 19).

Rice. 19. Period illustration

There are quite a lot of trigonometric formulas in the school course, but by and large it is enough to remember just one (Fig. 20).

Rice. 20. Trigonometric formulas

The double angle formula can also be easily derived from the sine of the sum by substituting (similarly for the cosine). You can also derive product formulas.

In fact, you need to remember very little, since with solving problems these formulas themselves will be remembered. Of course, someone will be too lazy to decide much, but then he will not need this technique, and therefore the formulas themselves.

And since the formulas are not needed, then there is no need to memorize them. You just need to understand the idea that trigonometric functions are functions that are used to calculate, for example, bridges. Almost no mechanism can do without their use and calculation.

1. The question often arises whether wires can be absolutely parallel to the ground. Answer: no, they cannot, since one force acts downward and the others act in parallel - they will never balance (Fig. 21).

2. A swan, a crayfish and a pike pull a cart in the same plane. The swan flies in one direction, the crayfish pulls in the other, and the pike in the third (Fig. 22). Their powers can be balanced. This balancing can be calculated using trigonometric functions.

3. Cable-stayed bridge (Fig. 23). Trigonometric functions help calculate the number of cables, how they should be directed and tensioned.

Rice. 23. Cable-stayed bridge

Rice. 24. “String Bridge”

Rice. 25. Bolshoi Obukhovsky Bridge

Links to site ma-te-ri-a-lyInternetUrok

Mathematics 6th grade:

Geometry 8th grade: