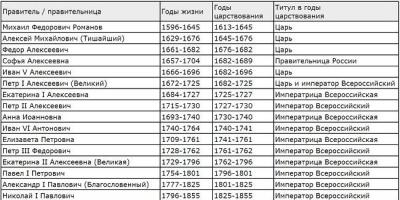
"Tasks for signs of similarity of triangles" - Similarity of triangles. Determining the height of an object using a mirror. Determining the height of an object from a puddle. Solution of practical problems. The shadow of the stick. Determining the height of an object. Measuring the height of large objects. Lesson motto. Solution of problems according to ready-made drawings. Independent work. Gymnastics for the eyes. Thales method. Individual card. Determining the height of the pyramid. Name similar triangles.
"Properties of quadrilaterals" - Names of quadrilaterals. All angles are right. Properties of quadrilaterals. Trapeze. A square is a rectangle in which all sides are equal. Elements of a parallelogram. Diagonals bisect the corners. Quadrilateral. Dictation. Diagonal. opposite corners. Help Dunno fix the deuce. Historical information. Quadrilaterals and their properties. Diagonals. Rhombus. opposite sides. Parties.
"Rhombus" - Signs. Perimeter. The appearance of the rhombus. Rhombus story. Rhombus. A rhombus with diagonals. What is a rhombus. Area formula. Interesting Facts. Rhombus properties. Rhombus in life.
"The solution of the Pythagorean theorem" - Proof by decomposition. Square area. The simplest proof. Proof of Perigal. Pythagoreans. Diagonal. 9th century CE proof followers. Height. Diameter. Complete proof. Motive. Hexagons. Proof by subtraction. Square. Rectangle. Possibilities of application of the theorem. Gutheil's proof. Application of the theorem. Lotus problem. History of the theorem.
"Area of a rectangle" grade 8 "- The area of \u200b\u200bthe square is equal to the square of its side. Square. Find the area and perimeter of the square. Area units. A polygon is made up of several polygons. Find the area of a triangle. The sides of each of the rectangles. Units. Find the area of the square. ABCD and DSMK are squares. The area of a rhombus is half the product of its diagonals. A parallelogram is drawn on side AB. Find the area of the hexagon.
"Trapezoid" Grade 8 "- The trapezius muscles of both sides of the back together have the shape of a trapezoid. Tasks for oral work. Are quadrilaterals trapezoids. Properties of an isosceles trapezoid. Signs of an isosceles trapezoid. Types of trapezoid. The area of the trapezoid. Trapeze elements. Definition. The median line of the trapezium. Trapeze. The geometric figure was named so for its resemblance to a small table.
Rhombus is one of the simplest geometric shapes. We so often meet with a rhombus in geometric problems that the words "fantastic" and "rhombus" seem to us incompatible concepts. Meanwhile, the amazing, as they say, is nearby ... in Britain. But first, let's remember what a "rhombus" is, its signs and properties.
The term "rhombus" in translation from ancient Greek means "tambourine". And this is no coincidence. And here's the thing. A tambourine at least once in a lifetime, but everyone saw it. And everyone knows that it is round. But a long time ago, tambourines were made just in the shape of a square or a rhombus. Moreover, the name of the diamond suit is also associated with this fact.
From geometry, we imagine what a rhombus looks like. This is a quadrilateral, which is depicted as an inclined square. But in no case should you confuse a rhombus and a square. It would be more correct to say that a rhombus is special case parallelogram. The only difference is that all sides of the rhombus are equal. To quickly and correctly solve problems in geometry, you need to remember the properties of a rhombus. By the way, a rhombus has all the properties of a parallelogram. So:
Rhombus properties:
- opposite sides are equal;
- opposite angles are equal;
- the diagonals of the rhombus intersect under the straight line and are divided in half at the point of intersection;
- the sum of the angles adjacent to one side is 180°;
- the sum of the squares of the diagonals is equal to the sum of the squares of all the sides;
- the diagonals are the bisectors of its angles.
Signs of a rhombus:
- if the diagonals of a parallelogram are perpendicular, then the parallelogram is a rhombus;
- if the diagonal of a parallelogram is the bisector of its angle, then the parallelogram is a rhombus.
And one more important point, without the knowledge of which it is not possible to successfully solve the problem - formulas. Below are the formulas for finding the area of any rhombus, which are used depending on the known data: height, diagonal, side, radius of the inscribed circle. In the following formulas, conventions: a - side of the rhombus, h a - height drawn to side a, A- the angle between the sides, d 1 d 2 - the diagonals of the rhombus.
Basic formulas:
S = a 2 sin A
S = 1/2 (d 1 d 2)
S = 4r2 / sin a
There is another formula that is not used so often, but is useful:
d 1 2 + d 2 2 = 4a 2 or the sum of the squares of the diagonals is equal to the square of the side times 4.
And now it's time to go back to the very beginning. What is so amazing 
maybe in this figurine? It turns out that in the 19th century, during archaeological excavations, a rhombus was found. Yes, not simple, but golden, and, in the truest sense of the word! This find from the British mound Bash was found in the Wilsford area, not far from the famous Stonehenge. The mysterious rhombus is a polished plate on which unusual patterns are engraved. Its size is 15.2 x 17.8 cm (rhombus with only a small reservation). In addition to the edging, the plate has three more smaller diamond-shaped patterns, which are supposedly nested into each other. At the same time, a rhombic grid is engraved in the center of the latter. Along the edges of the rhombus is a chevron pattern - nine characters on each side of the rhombus. There are thirty-six such triangles in total.
Of course, this product is very expensive, but it is also obvious that the creation of such a rhombus pursued a specific goal. That's just what, scientists could not figure out for a long time.
One of the more plausible and accepted versions concerns Stonehenge directly. It is known that the constructions of Stonehenge were erected gradually, over several centuries. It is believed that construction began around 3000 BC. It should be noted that gold in Britain became known already somewhere from 2800 BC. From this it can be assumed that the golden rhombus could well have been a priest's tool. In particular, the vizier. Such a hypothesis was brought to the attention of modern scientists by Professor A. Tom, a well-known researcher of Stonehenge, in the last quarter of the 20th century.
Not everyone can imagine that the ancient builders could accurately determine the angles on the ground. Nevertheless, the English researcher D. Furlong proposed a method that, in his opinion, the ancient Egyptians could use. Furlong believed that our ancestors used pre-selected aspect ratios in right triangles. After all, it has long been known that the Egyptians widely used a triangle with sides of three, four and five dimensional units. Apparently, the ancient inhabitants of the British Isles also knew many such tricks.
Well, even if you imagine that the people who built Stonehenge were excellent surveyors, how could a golden diamond help them in this? Hardly any modern surveyor will be able to answer this question. Most likely, the fact that Furlong was a surveyor by profession, gave him the opportunity to solve this riddle. After careful study, the researcher came to the conclusion that the polished gold rhombus with markings is excellent for use as a reflector of sunlight, in other words, a special dimensional mirror.
It was proved that in order to quickly determine the azimuth on the ground with fairly small errors, it was necessary to use two similar mirrors. The scheme was as follows: one priest, for example, stood on the top of one hill, and the other in the adjacent valley. It was also necessary to pre-set the distance between the priests. This can be done with just a few steps. Although they usually used a measuring stick, since the results were more reliable. Two diamond-shaped metal mirrors provide a right angle. And then it is easy to measure almost any required angles. D. Furlong even gave a table of such pairs of integers, which allows you to set any angle with an error of one degree. It is most likely that the priests of the Stonehenge era used this method. Of course, to confirm this hypothesis, it would be necessary to find a second, paired golden rhombus, but, apparently, this is not worth it. After all, the evidence is quite clear. In addition to calculating azimuths on the ground, another ability of an amazing golden rhombus was discovered. This amazing little thing is allowed to calculate the moments of the winter and summer solstices, spring and autumn equinoxes. This was an indispensable quality for the life of the ancient Egyptians, who worshiped then primarily the Sun.
It is likely that the impressive appearance of the rhombus was not only indispensable tool for priests, but was also a spectacular decoration for its owner. Generally speaking, the vast majority of jewelry found at first glance, expensive today, are, as it turns out later, measuring instruments.
So people have always been drawn to the unknown. And, judging by the fact that so much remains mysterious and unproven in our world, a person will try to find the clues to antiquity for a long time to come. And it's very cool! After all, we can learn a lot from our ancestors. To do this, you need to know a lot, be able to learn and learn. But it is impossible to become such a highly qualified specialist without basic knowledge. After all, after all, every great archaeologist, discoverer once went to school!
site, with full or partial copying of the material, a link to the source is required.
AB \parallel CD,\;BC \parallel AD
AB=CD,\;BC=AD
2. The diagonals of the rhombus are perpendicular.
AC\perp BD
Proof
Since a rhombus is a parallelogram, its diagonals are bisected.
So \triangle BOC = \triangle DOC on three sides (BO = OD , OC is joint, BC = CD ). We get that \angle BOC = \angle COD , and they are adjacent.
\Rightarrow \angle BOC = 90^(\circ) and \angle COD = 90^(\circ) .
3. The intersection point of the diagonals bisects them.
AC=2\cdot AO=2\cdot CO
BD=2\cdot BO=2\cdot DO
4. The diagonals of a rhombus are the bisectors of its angles.
\angle1 = \angle2; \; \angle 5 = \angle 6;
\angle 3 = \angle 4; \; \angle 7 = \angle 8.
Proof
Due to the fact that the diagonals are divided by the intersection point in half, and all sides of the rhombus are equal to each other, the whole figure is divided by the diagonals into 4 equal triangles:
\triangle BOC, \; \triangle BOA, \; \triangle AOD, \; \triangle COD.
This means that BD , AC are bisectors.
5. Diagonals form 4 right-angled triangles from a rhombus.
6. Any rhombus can contain a circle centered at the point of intersection of its diagonals.
7. The sum of the squares of the diagonals is equal to the square of one of the sides of the rhombus multiplied by four
AC^2 + BD^2 = 4\cdot AB^2
Signs of a rhombus
1. A parallelogram with perpendicular diagonals is a rhombus.
\begin(cases) AC \perp BD \\ ABCD \end(cases)- parallelogram, \Rightarrow ABCD - rhombus.
Proof
ABCD is a parallelogram \Rightarrow AO = CO ; BO=OD. It is also indicated that AC \perp BD \Rightarrow \triangle AOB = \triangle BOC = \triangle COD = \triangle AOD- on 2 legs.
It turns out that AB = BC = CD = AD.
Proven!
2. When in a parallelogram at least one of the diagonals divides both angles (through which it passes) in half, then this figure will be a rhombus.
Proof
On a note: not every figure (quadrilateral) with perpendicular diagonals will be a rhombus.
Eg:
This is no longer a rhombus, despite the perpendicularity of the diagonals.
To distinguish it, it is worth remembering that at first the quadrilateral must be a parallelogram and have
1. - straight. Accordingly, the solution of the inequality 
, is a half-plane lying below or above this line.
2. 
- hyperbole, because from here 
. This hyperbola divides the plane into 3 (!!!) regions, so the inequality sign must be checked in each of them.
3. 
- "recumbent parabola", i.e. parabola rotated 90 
clockwise. Divides the plane into 2 parts (inside the parabola and outside it.)
4.
- circle centered at the origin, radius R (where R>0). Inequality solution 
is a circle (i.e., the entire area lying inside the circle, together with the boundary), and the inequalities 
- the area outside the circle. 5. 
- for a > 0 - a square with vertices at the points (a; 0), (0; a), (-a; 0), (0; -a). Accordingly, the solution of the inequality 
is the area inside the square, and the inequalities 
- the area outside the square.
Graph transformations:
1
f(x-a; y-b)=0, you must first plot the equation f(x; y)=0, and then shift it by A units along the axis Oh, and on b units along the Oy axis.
2
. To plot the equation 
, it is necessary to fulfill the symmetry of the graph of the equation f(x; y) = 0 with respect to the Oy axis (while not forgetting to erase the part of the original graph that lies to the left of the Oy axis).
3
. To plot the equation 
, it is necessary to fulfill the symmetry of the graph of the equation f(x; y) = 0 with respect to the Ox axis (while not forgetting to erase the part of the original graph that lies below the Ox axis).
4.
Accordingly, to plot the equation 
, you must first plot the equation f(x; y)=0 (i.e. remove all modules) in first quarter, and then perform the symmetry of this graph about all axes.
Inequalities with two variables.
Most often, the “area method” is used to solve. That is, first, in the inequality, the inequality sign is replaced with the “=” sign and the resulting graph is displayed on the coordinate plane. Then, using the “trial point method”, the inequality sign is checked in each of the formed areas.
In addition, one can separately consider inequalities of the form 
And 
. To solve them, we first build a graph of the function 
. Then the solution of the first inequality will be the points lying below this graph, and the solution of the second one, respectively, will be the points lying above.
One can also single out inequalities of the form 
. (The inequality sign may be different.) To solve it, you need to draw a graph with a solid line equations 
and dotted line - graph equations 
and check the inequality sign in each resulting region (selecting any point from each region).
Example 1
№ 9.20 (d)
Figure Solution of Inequality 
and determine all values of a for which the given inequality has at least one solution.
Solution.
This inequality is equivalent to the following:
.
To do this, we first construct a graph of the equation
.
a) In turn, to construct this graph, we will use rule 4 of graph transformation. Here f(x; a) = 5x + 2a . The graph of this equation is a straight line that intersects the coordinate axes at points (2, 0) and (0, 5). Because we consider the case without modules (i.e. x 
and y), then we take only the part of this line that lies in the first quadrant.
b) to build a graph of the equation , we perform the symmetry of the resulting segment with respect to all coordinate axes and the origin. We get a rhombus with a "center" at the origin.
b) Now let's shift this graph 3 units to the right and 1 unit down.
We got the graph of the equation
We see that the coordinate plane was divided into 2 regions, inside the rhombus and outside it. We see that, for example, the point (3,-1) belongs to the inner region. Substitute its coordinates into inequality. We make sure that the inequality at this point is satisfied. Hence, all points of this region satisfy the inequality. To check, we also substitute a point from the outer region into the inequality. For example, this is the point (0, 8). For the given values of the variables, the inequality turns into an incorrect numerical inequality, which means that no point from the outer region satisfies the inequality. Finally, we obtain that the solution of the inequality is the “inside” of the rhombus. We show this with shading.
Answer: this inequality has a solution for
Example 2. Draw on the coordinate plane a set of points that satisfy the inequality 
.
Solution
1. Let's build the lines bounding the graph of inequality. These will be lines that are the image of the sets of those points at which the numerator and denominator turn to 0. I.e. plot the graphs of the equations
(A)
And 
(B)
A) The graph of this equation is a circle with a center at the point (2, -3) and a radius equal to 4 - it is depicted as a solid line, because the inequality is not strict.
B) The graph of this equation - a "lying parabola", lowered by 1 unit down - is depicted by a dotted line due to the domain of the inequality.
2. Let ,
. Then our inequality becomes 
.
The circle and the parabola divide the coordinate plane into 4 regions.
Note that the area inside the circle corresponds to the inequality
, i.e. 
. The area outside the circle - inequality 
, i.e. 
.
Similarly, the area "inside" or to the right of the parabola corresponds to the inequality 
or 
, and the area “outside”, or to the left of the parabola, to the inequality 
or 
.
And, finally, in the region IV and , i.e. the fraction is non-positive and the inequality is not satisfied.
Thus, the solution to the inequality is the union of regions I and III. 
